記事の概要
今回はハイゼンベルグモデルの2粒子系(ダイマー)の計算
大学で物理をやってました。ちょっと懐かしくなってコード書いて見ました(^_^)
この記事の前提
-
言語はPythonで書きます
-
数値計算の方法について書いてます
-
学術的に、ハイゼンベルグモデル・2粒子系が何かについて説明はしてません
-
間違いがある可能性があります。あらかじめご了承くださいm( )m
結論
計算の流れ
- ハミルトニアンを行列表示
- bitをスピンに対応させて計算 → 論理演算子を利用
- 求めたハミルトニアンの固有値・固有ベクトルを計算
- 固有エネルギー・固有状態が求められる
コードと実行結果
今回はJ = 1で計算
\begin{equation}
\mathcal{H} = J\sum_{ij}{\vec{S_i}\cdot\vec{S_j}} = J\sum{(S_i^zS_j^z + \frac{1}{2}(S_i^+S_j^- + S_i^-S_j^+))}
\end{equation}
※何故か2番目の$\sum$にMARKDOWN_HASH7bed657a775c37c2570786d0cbeefd88MARKDOWNHASHが付けられません(^^;)
※簡略化のためJ = 1で計算
コード
import numpy as np
def get_bit(input_state, i):
# 取り出したいbitだけ立てる
target_bit = input_state & 2 ** i
# 0 or 1を取り出す
target_bit = target_bit >> i
return target_bit
if __name__ == '__main__':
H = np.zeros((2 ** 2, 2 ** 2))
for state in range(2 ** 2):
init_state = state
# Jz計算
temp_bit = 0
Jz = 1.0
for s_i in range(2):
temp_bit = get_bit(state, s_i)
Jz = Jz * 0.5 * (2 * temp_bit - 1)
H[state][state] = H[state][state] + Jz
# (Ji+Jj- + Ji-Jj+) / 2 の計算
temp_bit_J1 = get_bit(state, 0)
temp_bit_J2 = get_bit(state, 1)
if temp_bit_J1 != temp_bit_J2:
target_bits = 2**0 + 2**1
target_element = state ^ target_bits
H[target_element][state] = 0.5
print("matrix")
print(H)
test_eig, test_v = np.linalg.eig(H)
print("eigen value")
print(test_eig)
print("eigen state")
print(test_v)実行結果
matrix
[[ 0.25 0. 0. 0. ]
[ 0. -0.25 0.5 0. ]
[ 0. 0.5 -0.25 0. ]
[ 0. 0. 0. 0.25]]
eigen value
[ 0.25 -0.75 0.25 0.25]
eigen state
[[ 0. 0. 1. 0. ]
[ 0.70710678 0.70710678 0. 0. ]
[ 0.70710678 -0.70710678 0. 0. ]
[ 0. 0. 0. 1. ]]memo(≒解説)
コンセプト
- 電子状態をbit(0 or 1)で表現
0 = ↓、1 = ↑でスピンを表現- ここは決めるだけなのでどちらでもOK(磁場をかける際は気をつける)
- ダイマーのとりうる状態|↓↓>、|↑↓>、|↓↑>、|↑↑>は0~3(00~11)で表現できる
- |↓↓>、|↑↓>、|↓↑>、|↑↑>でハミルトニアンを行列表現
- 求めたハミルトニアンから固有値・固有状態を求める
$\mathcal{H}$|↓↓>、$\mathcal{H}$|↑↓>、$\mathcal{H}$|↓↑>、$\mathcal{H}$|↑↑>のループ処理
ハミルトニアン
$$
\mathcal{H} = J\sum_{ij}{\vec{S_i}・\vec{S_j}}
= J\sum(S_i^zS_j^z + \frac{1}{2}(S_i^+S_j^- + S_i^-S_j^+))
$$
※何故か2番目の$\sum$にMARKDOWN_HASH7bed657a775c37c2570786d0cbeefd88MARKDOWNHASHが付けられません(^^;)
で計算
- 簡単のため
J = 1で計算 - |↓↓>、|↑↓>、|↓↑>、|↑↑> → 00、01、10、11(2進数)
- 整数0 ~ 3でループ処理
for state in range(2 ** 2):0 or 1の判定
- 今回はハミルトニアン計算で1番目、2番目の状態(=bit)が0か1か判定する必要がある
- 複数箇所で必要なため、クラス化した
def get_bit(input_state, i):
# 取り出したいbitだけ立てる
target_bit = input_state & 2 ** i
# 0 or 1を取り出す
target_bit = target_bit >> i
return target_bit$S_i^zS_j^z$の計算
- n番目のbitが0 or 1で $±\frac{1}{2}$ をとる
- 各bit毎の値の積
# Sz計算
temp_bit = 0
Jz = 1.0
for s_i in range(2):
temp_bit = get_bit(state, s_i)
Jz = Jz * 0.5 * (2 * temp_bit - 1)
H[state][state] = H[state][state] + Jz$S_i^+S_j^- + S_i^-S_j^+$の計算
- 要するにi番目、j番目のビット状態の入れ替え
- 揃っていたら作用しない(= 0になる)
- たとえば<↑↓|$\mathcal{H}$|↓↑>に$\frac{1}{2}J$ (今回はJ = 1)が入る
# (Ji+Jj- + Ji-Jj+) / 2 の計算
temp_bit_J1 = get_bit(state, 0)
temp_bit_J2 = get_bit(state, 1)
if temp_bit_J1 != temp_bit_J2:
target_bits = 2**0 + 2**1
target_element = state ^ target_bits
H[target_element][state] = 0.5固有値・固有状態の計算
※ 今回はJ = 1で計算
- 行列表現したハミルトニアンの固有値と固有状態を求める
→ 固有エネルギーと固有状態が求められる - 今回はライブラリ(NumPy)を利用
test_eig, test_v = np.linalg.eig(H)コード例だと
test_eig→固有値test_v→固有状態
になる
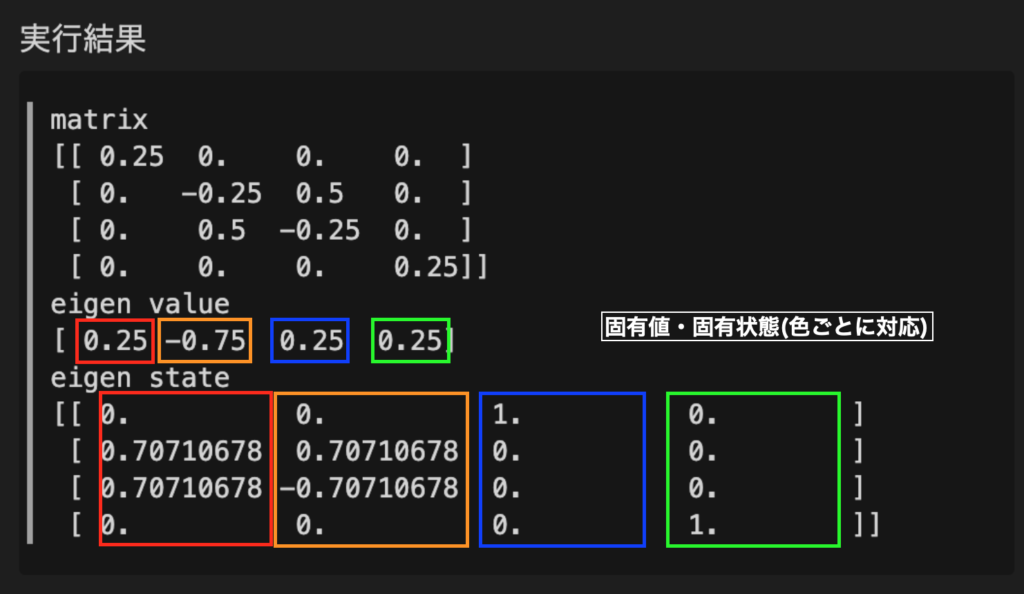
確認した感じだと、上の図のように固有値・固有状態が対応している
まとめ
- Pythonでビットの論理演算子を使ってスピン状態の計算をした
- 求めた行列をライブラリを使用し、固有エネルギー(固有値)・固有状態(固有ベクトル)を求めた
コメント